Quantitative Data Analysis 101
A Plain-Language Explainer With Examples + Free Template 📝
By: Derek Jansen (MBA) and Kerryn Warren (PhD) | Updated March 2025

The good news is that while quantitative data analysis is a mammoth topic, gaining a working understanding of the basics isn’t that hard, even for those of us who avoid numbers and math. In this post, we’ll break quantitative analysis down into simple, bite-sized chunks so you can approach your research with confidence.
Overview: Quantitative Data Analysis 101
What is quantitative data analysis?
Despite being a mouthful, quantitative data analysis simply means analysing data that is numbers-based – or data that can be easily “converted” into numbers without losing any meaning.
For example, category-based variables like gender, ethnicity, or native language could all be “converted” into numbers without losing meaning – for example, English could equal 1, French 2, etc.
This contrasts against qualitative data analysis, where the focus is on words, phrases and expressions that can’t be reduced to numbers. If you’re interested in learning about qualitative analysis, check out our post and video here.
What is quantitative analysis used for?
Quantitative analysis is generally used for three purposes.
- Firstly, it’s used to measure differences between groups. For example, the popularity of different clothing colours or brands.
- Secondly, it’s used to assess relationships between variables. For example, the relationship between weather temperature and voter turnout.
- And third, it’s used to test hypotheses in a scientifically rigorous way. For example, a hypothesis about the impact of a certain vaccine.
Again, this contrasts with qualitative analysis, which can be used to analyse people’s perceptions and feelings about an event or situation. In other words, things that can’t be reduced to numbers.
How does quantitative analysis work?
Well, since quantitative data analysis is all about analysing numbers, it’s no surprise that it involves statistics. Statistical analysis methods form the engine that powers quantitative analysis, and these methods can vary from pretty basic calculations (for example, averages and medians) to more sophisticated analyses (for example, correlations and regressions).
Sounds like gibberish? Don’t worry. We’ll explain all of that in this post. Importantly, you don’t need to be a statistician or math wiz to pull off a good quantitative analysis. We’ll break down all the technical mumbo jumbo in this post.
The two “branches” of quantitative analysis
As I mentioned, quantitative analysis is powered by statistical analysis methods. There are two main “branches” of statistical methods that are used – descriptive statistics and inferential statistics. In your research, you might only use descriptive statistics, or you might use a mix of both, depending on what you’re trying to figure out. In other words, depending on your research questions, aims and objectives. I’ll explain how to choose your methods later.
So, what are descriptive and inferential statistics?
Well, before I can explain that, we need to take a quick detour to explain some lingo. To understand the difference between these two branches of statistics, you need to understand two important words. These words are population and sample.
First up, population. In statistics, the population is the entire group of people (or animals or organisations or whatever) that you’re interested in researching. For example, if you were interested in researching Tesla owners in the US, then the population would be all Tesla owners in the US.
However, it’s extremely unlikely that you’re going to be able to interview or survey every single Tesla owner in the US. Realistically, you’ll likely only get access to a few hundred, or maybe a few thousand owners using an online survey. This smaller group of accessible people whose data you actually collect is called your sample.
So, to recap – the population is the entire group of people you’re interested in, and the sample is the subset of the population that you can actually get access to. In other words, the population is the full chocolate cake, whereas the sample is a slice of that cake.
So, why is this sample-population thing important?
Well, descriptive statistics focus on describing the sample, while inferential statistics aim to make predictions about the population, based on the findings within the sample. In other words, we use one group of statistical methods – descriptive statistics – to investigate the slice of cake, and another group of methods – inferential statistics – to draw conclusions about the entire cake. There I go with the cake analogy again…
With that out the way, let’s take a closer look at each of these branches in more detail.

Branch 1: Descriptive Statistics
Descriptive statistics serve a simple but critically important role in your research – to describe your data set – hence the name. In other words, they help you understand the details of your sample. Unlike inferential statistics (which we’ll get to soon), descriptive statistics don’t aim to make inferences or predictions about the entire population – they’re purely interested in the details of your specific sample.
When you’re writing up your analysis, descriptive statistics are the first set of stats you’ll cover, before moving on to inferential statistics. But, that said, depending on your research objectives and research questions, they may be the only type of statistics you use. We’ll explore that a little later.
So, what kind of statistics are usually covered in this section?
Some common statistical tests used in this branch include the following:
- Mean – this is simply the mathematical average of a range of numbers.
- Median – this is the midpoint in a range of numbers when the numbers are arranged in numerical order. If the data set makes up an odd number, then the median is the number right in the middle of the set. If the data set makes up an even number, then the median is the midpoint between the two middle numbers.
- Mode – this is simply the most commonly occurring number in the data set.
- Standard deviation – this metric indicates how dispersed a range of numbers is. In other words, how close all the numbers are to the mean (the average).
- In cases where most of the numbers are quite close to the average, the standard deviation will be relatively low.
- Conversely, in cases where the numbers are scattered all over the place, the standard deviation will be relatively high.
- Skewness. As the name suggests, skewness indicates how symmetrical a range of numbers is. In other words, do they tend to cluster into a smooth bell curve shape in the middle of the graph, or do they skew to the left or right?
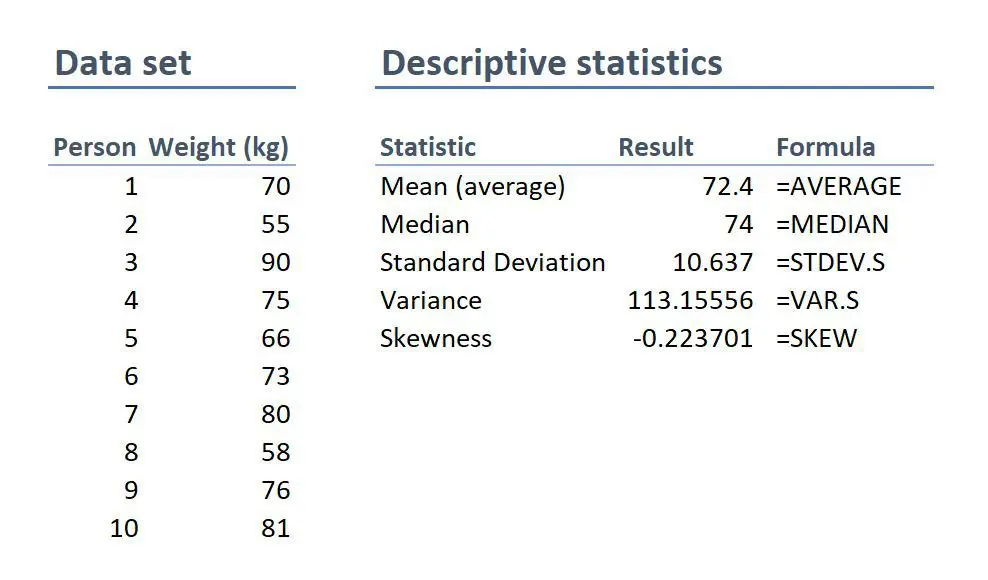
Feeling a bit confused? Let’s look at a practical example using a small data set.
First, we can see that the mean weight is 72.4 kilograms. In other words, the average weight across the sample is 72.4 kilograms. Straightforward.
Next, we can see that the median is very similar to the mean (the average). This suggests that this data set has a reasonably symmetrical distribution (in other words, a relatively smooth, centred distribution of weights, clustered towards the centre).
In terms of the mode, there is no mode in this data set. This is because each number is present only once and so there cannot be a “most common number”. If there were two people who were both 65 kilograms, for example, then the mode would be 65.
Next up is the standard deviation. 10.6 indicates that there’s quite a wide spread of numbers. We can see this quite easily by looking at the numbers themselves, which range from 55 to 90, which is quite a stretch from the mean of 72.4.
And lastly, the skewness of -0.2 tells us that the data is very slightly negatively skewed. This makes sense since the mean and the median are slightly different.
As you can see, these descriptive statistics give us some useful insight into the data set. Of course, this is a very small data set (only 10 records), so we can’t read into these statistics too much. Also, keep in mind that this is not a list of all possible descriptive statistics – just the most common ones.
First, we can see that the mean weight is 72.4 kilograms. In other words, the average weight across the sample is 72.4 kilograms. Straightforward.
Next, we can see that the median is very similar to the mean (the average). This suggests that this data set has a reasonably symmetrical distribution (in other words, a relatively smooth, centred distribution of weights, clustered towards the centre).
In terms of the mode, there is no mode in this data set. This is because each number is present only once and so there cannot be a “most common number”. If there were two people who were both 65 kilograms, for example, then the mode would be 65.
Next up is the standard deviation. 10.6 indicates that there’s quite a wide spread of numbers. We can see this quite easily by looking at the numbers themselves, which range from 55 to 90, which is quite a stretch from the mean of 72.4.
And lastly, the skewness of -0.2 tells us that the data is very slightly negatively skewed. This makes sense since the mean and the median are slightly different.
As you can see, these descriptive statistics give us some useful insight into the data set. Of course, this is a very small data set (only 10 records), so we can’t read into these statistics too much. Also, keep in mind that this is not a list of all possible descriptive statistics – just the most common ones.
While these descriptive statistics are all fairly basic, they’re important for a few reasons:
- Firstly, they help you get both a macro and micro-level view of your data. In other words, they help you understand both the big picture and the finer details.
- Secondly, they help you spot potential errors in the data – for example, if an average is way higher than you’d expect, or responses to a question are highly varied, this can act as a warning sign that you need to double-check the data.
- And lastly, these descriptive statistics help inform which inferential statistical techniques you can use, as those techniques depend on the skewness (in other words, the symmetry and normality) of the data.
Simply put, descriptive statistics are really important, even though the statistical techniques used are fairly basic. All too often at Grad Coach, we see students skimming over the descriptives in their eagerness to get to the more exciting inferential methods, and then landing up with some very flawed results.
Don’t be a sucker – give your descriptive statistics the love and attention they deserve!
I didn’t know if I was good enough.
See how Kelsee went from lost and confused to conquering her PhD.Branch 2: Inferential Statistics
As I mentioned, while descriptive statistics are all about the details of your specific data set – your sample – inferential statistics aim to make inferences about the population. In other words, you’ll use inferential statistics to make predictions about what you’d expect to find in the full population.
What kind of predictions, you ask? Well, there are two common types of predictions that researchers try to make using inferential stats:
- Firstly, predictions about differences between groups – for example, height differences between children grouped by their favourite meal or gender.
- And secondly, relationships between variables – for example, the relationship between body weight and the number of hours a week a person does yoga.
In other words, inferential statistics (when done correctly), allow you to connect the dots and make predictions about what you expect to see in the real world population, based on what you observe in your sample data. For this reason, inferential statistics are used for hypothesis testing – in other words, to test hypotheses that predict changes or differences.

For example, if your population of interest is a mix of 50% male and 50% female, but your sample is 80% male, you can’t make inferences about the population based on your sample, since it’s not representative. This area of statistics is called sampling, but we won’t go down that rabbit hole here (it’s a deep one!) – we’ll save that for another post.
There are many, many different statistical analysis methods within the inferential branch and it’d be impossible for us to discuss them all here. So we’ll just take a look at some of the most common inferential statistical methods so that you have a solid starting point.
First up are T-Tests. T-tests compare the means (the averages) of two groups of data to assess whether they’re statistically significantly different. In other words, do they have significantly different means, standard deviations and skewness.
This type of testing is very useful for understanding just how similar or different two groups of data are. For example, you might want to compare the mean blood pressure between two groups of people – one that has taken a new medication and one that hasn’t – to assess whether they are significantly different.
Kicking things up a level, we have ANOVA, which stands for “analysis of variance”. This test is similar to a T-test in that it compares the means of various groups, but ANOVA allows you to analyse multiple groups, not just two groups So it’s basically a t-test on steroids…
Next, we have correlation analysis. This type of analysis assesses the relationship between two variables. In other words, if one variable increases, does the other variable also increase, decrease or stay the same. For example, if the average temperature goes up, do average ice creams sales increase too? We’d expect some sort of relationship between these two variables intuitively, but correlation analysis allows us to measure that relationship scientifically.
Lastly, we have regression analysis – this is quite similar to correlation in that it assesses the relationship between variables, but it goes a step further to understand cause and effect between variables, not just whether they move together. In other words, does the one variable actually cause the other one to move, or do they just happen to move together naturally thanks to another force? Just because two variables correlate doesn’t necessarily mean that one causes the other.
I hear you. To make this all a little more tangible, let’s take a look at an example of a correlation in action.
Here’s a scatter plot demonstrating the correlation (relationship) between weight and height. Intuitively, we’d expect there to be some relationship between these two variables, which is what we see in this scatter plot. In other words, the results tend to cluster together in a diagonal line from bottom left to top right.
For example, some methods only work with normally distributed (parametric) data, while other methods are designed specifically for non-parametric data. And that’s exactly why descriptive statistics are so important – they’re the first step to knowing which inferential techniques you can and can’t use.

How to choose the right analysis method
To choose the right statistical methods, you need to think about two important factors:
- The type of quantitative data you have (specifically, level of measurement and the shape of the data). And,
- Your research questions and hypotheses
Let’s take a closer look at each of these.
Factor 1 – Data type
The first thing you need to consider is the type of data you’ve collected (or the type of data you will collect). By data types, I’m referring to the four levels of measurement – namely, nominal, ordinal, interval and ratio. If you’re not familiar with this lingo, check out the video below.

Well, because different statistical methods and techniques require different types of data. This is one of the “assumptions” I mentioned earlier – every method has its assumptions regarding the type of data.
For example, some techniques work with categorical data (for example, yes/no type questions, or gender or ethnicity), while others work with continuous numerical data (for example, age, weight or income) – and, of course, some work with multiple data types.
If you try to use a statistical method that doesn’t support the data type you have, your results will be largely meaningless. So, make sure that you have a clear understanding of what types of data you’ve collected (or will collect). Once you have this, you can then check which statistical methods would support your data types here.
If you haven’t collected your data yet, you can work in reverse and look at which statistical method would give you the most useful insights, and then design your data collection strategy to collect the correct data types.
Another important factor to consider is the shape of your data. Specifically, does it have a normal distribution (in other words, is it a bell-shaped curve, centred in the middle) or is it very skewed to the left or the right? Again, different statistical techniques work for different shapes of data – some are designed for symmetrical data while others are designed for skewed data.
This is another reminder of why descriptive statistics are so important – they tell you all about the shape of your data.
Factor 2: Your research questions
The next thing you need to consider is your specific research questions, as well as your hypotheses (if you have some). The nature of your research questions and research hypotheses will heavily influence which statistical methods and techniques you should use.
If you’re just interested in understanding the attributes of your sample (as opposed to the entire population), then descriptive statistics are probably all you need. For example, if you just want to assess the means (averages) and medians (centre points) of variables in a group of people.
On the other hand, if you aim to understand differences between groups or relationships between variables and to infer or predict outcomes in the population, then you’ll likely need both descriptive statistics and inferential statistics.
So, it’s really important to get very clear about your research aims and research questions, as well your hypotheses – before you start looking at which statistical techniques to use.
Never shoehorn a specific statistical technique into your research just because you like it or have some experience with it. Your choice of methods must align with all the factors we’ve covered here.
Time to recap…
You’re still with me? That’s impressive. We’ve covered a lot of ground here, so let’s recap on the key points:
- Quantitative data analysis is all about analysing number-based data (which includes categorical and numerical data) using various statistical techniques.
- The two main branches of statistics are descriptive statistics and inferential statistics. Descriptives describe your sample, whereas inferentials make predictions about what you’ll find in the population.
- Common descriptive statistical methods include mean (average), median, standard deviation and skewness.
- Common inferential statistical methods include t-tests, ANOVA, correlation and regression analysis.
- To choose the right statistical methods and techniques, you need to consider the type of data you’re working with, as well as your research questions and hypotheses.
Learn More About Quantitative:

Triangulation: The Ultimate Credibility Enhancer
Triangulation is one of the best ways to enhance the credibility of your research. Learn about the different options here.

Inferential Statistics 101: Simple Explainer (With Examples)
Learn about the key concepts and tests within inferential statistics, including t-tests, ANOVA, chi-square, correlation and regression.

Descriptive Statistics 101: Simple Explainer (With Examples)
Learn about the key concepts and measures within descriptive statistics, including measures of central tendency and dispersion.

Validity & Reliability: Explained Simply
Learn about validity and reliability within the context of research methodology. Plain-language explainer video with loads of examples.

Research Design 101: Qualitative & Quantitative
Learn about research design for both qualitative and quantitative studies. Includes plain-language explanations and examples.



Hi,
I have read your article. Such a brilliant post you have created.
Thank you for the feedback. Good luck with your quantitative analysis.
Thank you so much.
Thank you so much. I learnt much well. I love your summaries of the concepts. I had love you to explain how to input data using SPSS
Very useful, I have got the concept
Amazing and simple way of breaking down quantitative methods.
This is beautiful….especially for non-statisticians. I have skimmed through but I wish to read again. and please include me in other articles of the same nature when you do post. I am interested. I am sure, I could easily learn from you and get off the fear that I have had in the past. Thank you sincerely.
Send me every new information you might have.
i need every new information
Thank you for the blog. It is quite informative.
Dr Peter Nemaenzhe PhD
It is wonderful. l’ve understood some of the concepts in a more compréhensive manner
Hi,
Your article is so good! However, I am still a bit lost. I am doing a secondary research on Gun control in the US and increase in crime rates and I am not sure which analysis method I should use?
Based on the given learning points, this is inferential analysis, thus, use ‘t-tests, ANOVA, correlation and regression analysis’
Amazing
Well explained notes. Am an MPH student and currently working on my thesis proposal, this has really helped me understand some of the things I didn’t know.
I like your page..helpful
wonderful i got my concept crystal clear. thankyou!!
This is really helpful , thank you
Thank you so much this helped
Wonderfully explained
thank u so much, it was so informative
THANKYOU, this was very informative and very helpful
This is great GRADACOACH
I am not a statistician but I require more of this in my thesis
Include me in your posts.
Thank you
This is so great and fully useful. I would like to thank you again and again.
Glad to read this article. I’ve read lot of articles but this article is clear on all concepts. Thanks for sharing.
Send me every new information you might have.
Thank you so much. This is a very good foundation and intro into quantitative data analysis. Appreciate!
You have a very impressive, simple but concise explanation of data analysis for Quantitative Research here. This is a God-send link for me to appreciate research more. Thank you so much!
Avery good presentation followed by the write up. yes you simplified statistics to make sense even to a layman like me. Thank so much keep it up. The presenter did ell too. i would like more of this for Qualitative and exhaust more of the test example like the Anova.
This is a very helpful article, couldn’t have been clearer. Thank you.
Awesome and phenomenal information.Well done
The video with the accompanying article is super helpful to demystify this topic. Very well done. Thank you so much.
thank you so much, your presentation helped me a lot
I don’t know how should I express that ur article is saviour for me 🥺😍
It is well defined information and thanks for sharing. It helps me a lot in understanding the statistical data.
I gain a lot and thanks for sharing brilliant ideas, so wish to be linked on your email update.
Very helpful and clear .Thank you Gradcoach.
Thank for sharing this article, well organized and information presented are very clear.
VERY INTERESTING AND SUPPORTIVE TO NEW RESEARCHERS LIKE ME. AT LEAST SOME BASICS ABOUT QUANTITATIVE.
An outstanding, well explained and helpful article. This will help me so much with my data analysis for my research project. Thank you!
wow this has just simplified everything i was scared of how i am gonna analyse my data but thanks to you i will be able to do so
simple and constant direction to research. thanks
This is helpful
Great writing!! Comprehensive and very helpful.
Do you provide any assistance for other steps of research methodology like making research problem testing hypothesis report and thesis writing?
Thank you so much for such useful article!
Amazing article. So nicely explained. Wow
Very insightfull. Thanks
I am doing a quality improvement project to determine if the implementation of a protocol will change prescribing habits. Would this be a t-test?
The is a very helpful blog, however, I’m still not sure how to analyze my data collected. I’m doing a research on “Free Education at the University of Guyana”
tnx. fruitful blog!
So I am writing exams and would like to know how do establish which method of data analysis to use from the below research questions: I am a bit lost as to how I determine the data analysis method from the research questions.
Do female employees report higher job satisfaction than male employees with similar job descriptions across the South African telecommunications sector? – I though that maybe Chi Square could be used here.
– Is there a gender difference in talented employees’ actual turnover decisions across the South African
telecommunications sector? T-tests or Correlation in this one.
– Is there a gender difference in the cost of actual turnover decisions across the South African telecommunications
sector? T-tests or Correlation in this one.
– What practical recommendations can be made to the management of South African telecommunications companies on leveraging gender to mitigate employee turnover decisions?
Your assistance will be appreciated if I could get a response as early as possible tomorrow
This was quite helpful. Thank you so much.
wow I got a lot from this article, thank you very much, keep it up
Thanks for yhe guidance.
Can you send me this guidance on my email? To enable offline reading?
Thank you very much, this service is very helpful.
Every novice researcher needs to read this article as it puts things so clear and easy to follow. Its been very helpful.
Wonderful!!!! you explained everything in a way that anyone can learn. Thank you!!
I really enjoyed reading though this. Very easy to follow. Thank you
Hi,
Many thanks for your useful lecture, I would be really appreciated if you could possibly share with me the PPT of presentation related to Data type?
Thank you very much for sharing, I got much from this article
i LOVE IT
This is a very informative write-up. Kindly include me in your latest posts.
Very interesting mostly for social scientists
Thank you so much, very helpfull
You’re welcome 🙂
woow, its great, its very informative and well understood because of your way of writing like teaching in front of me in simple languages.
I have been struggling to understand a lot of these concepts. Thank you for the informative piece which is written with outstanding clarity.
very informative article. Easy to understand
Beautiful read, much needed.
Always greet intro and summary. I learn so much from GradCoach
Quite informative. Simple and clear summary.
I thoroughly enjoyed reading your informative and inspiring piece. Your profound insights into this topic truly provide a better understanding of its complexity. I agree with the points you raised, especially when you delved into the specifics of the article. In my opinion, that aspect is often overlooked and deserves further attention.
Absolutely!!! Thank you
Thank you very much for this post. It made me to understand how to do my data analysis.
its nice work and excellent job ,you have made my work easier
Wow!
So explicit. Well done.
This explanation is very clear and straight forward. Excellent job!
Thank you very much for this simplified and understandable explanation.
I think I’m learning things fast here. The concepts that I couldn’t get in my first degree program are now deeply understood and ready to teach and apply. THANK YOU VERY MUCH. THIS BLOG IS HELPING A LOT.
No one else could have simplified quantitative statistics in such a clear and engaging way. This article makes complex concepts feel incredibly accessible—truly impressive work.Heartiest congratulations